東京外国語大学 2013年度秋学期 金曜日5限目
教員名:Hermann Gottschewski
連絡先:gottschewskiアットfusehime.c.u-tokyo.ac.jp
科目名:総合文化研究入門A
テーマ:西洋音楽の文化史―ドイツの音楽を中心に
第7回(2013/12/06)
19世紀末・20世紀初頭の音楽(調性の危機を中心に)
前置き(が長いが、、、)
「調性の危機」を話すためにはまず調性(英tonality、独Tonalität、仏tonalité)の定義が必要になるだろう。しかしその場合には「調性の危機」を歴史的事実の一つとして扱わなければならない。従って、現在の立場から調性という概念を理解するのに一番合理的と思われる思想体系から論じるのではなく、その概念を歴史的に語らなければならない。つまり調性そのものだけではなく、調性の概念自体を歴史的に変化するものとして扱うので、全ての時代に対応できる一貫した定義はもとよりありえないこととなる。しかしここでは便宜のために三つの定義をまず設定したい。
1もっとも広義では、調性は一つの音組織の中で、音高の相互関係の原理を指す。この場合の「音組織」(独Tonsystem)は特定の音楽に使われる音高(ピッチ)とその相互関係を指す。「音組織」という単語には、音の相互関係には何かの原理があるということが暗示されている。従ってこの広義の概念によれば、何かの音組織に基づいている音楽は調性音楽である。それには例えば日本の伝統音楽も含まれる。また、一般的に「無調[性]音楽」と呼ばれる十二音技法の作品(シェーンベルクを中心とする「新ウィーン楽派」から発生した20世紀の音楽)も、この広義では調性音楽に含まれる。シェーンベルク自身はこういう広義の考え方の支持者で、十二音技法の曲が無調性だという解釈に賛成できなかった。
2より一般的な広義の解釈では、調性は一つの音組織の中で、音高の従属性(上下関係)を意味する。この意味での調性音楽には大体主音、終止音、中心音などと呼ばれる、上下関係で一番上位に位置する音が存在する。(ただしそういう音が複数存在したり、移動したりする例もこの意味での調性音楽に含めることができる。)この意味では教会旋法によるグレゴリオ聖歌、日本の伝統音楽の旋律等が調性音楽の概念に含まれるが、音高の従属性を否定する十二音技法は含まれない。
3もっとも狭義では、調性は近代西洋音楽の長調・短調の音組織に見られる特定の音高の従属性を意味する。それを代表する音楽理論としては主にフーゴ・リーマン(Hugo Riemann, 1849–1919)の機能和声論とハインリヒ・シェンカー(Heinrich Schenker,
1868–1935)の根本構造理論が挙げられる。この狭義の定義に従えば中世音楽や非西洋の伝統音楽等は調性音楽に含まれないことになる。
「調性の危機」という表現が意味するところは、西洋音楽史において中世から1900年ごろまで、調性の発展には2の広義の調性から3の狭義の調性への連続性があったが、その連続的な発展に限界が生じたことである。一部の作曲家(R・シュトラウス)は20世紀半ばまでもその限界を認めず更なる発展を目指し続けたが、多くの作曲家はさらなる発展をほとんど不可能なものとし、
・調性に関しての発展を全面的に諦める(S・ラフマニノフ、軽音楽、ポップス等)
・発展の連続性を諦めて、3の意味での調性を否定し、それ以前(少なくとも17世紀以前)の音楽に遡ったり(一部の教会音楽作曲家がその道を取った)、非西洋音楽の調性からヒントを得たり(ドビュッシー、ジャズ等)、理論的な新しい概念に基づいた音組織の導入したり(ブゾーニ、ヒンデミット等)して、出発点を改める
・もっとも革命的な方法として、2の意味での調性を全面的に否定し、その意味で「無調性」の、まったく新しい原理に従う十二音技法等を導入する(シェーンベルクを中心とする「新ウイーン楽派」、セリエル音楽等)
などの道を進んだ。従って「調性の危機」以前に西洋音楽で一般の音楽語法として統一的に発展していた調性にはもはや統一性がなくなり、調性は音楽のジャンルの問題となり、極端に言えば調性そのものが音楽表現内容の一つとなった。西洋音楽の「現代」がそこから始まるとも言える。
この根本的な変化の必要条件としては「古楽の美的現在性」(古い時代の音楽が一般に鑑賞されるという、19世紀前半頃から生じた事態)と「音楽的グローバル化」(非西洋音楽が西洋で一般的に知られる事態)という、調性の発展から見れば外的な理由も挙げることができるが、この講義では3の意味での調性の発展自体から生じた内的な理由に重点を置きながら説明したいと思う。ただしそれを一回の授業で扱うためにはかなりの簡略化が必要なので、今回は3の意味での調性を構成する基本要素の体系的従属性を話の軸にして、作曲技法と音楽理論の実際の歴史発展についてはできるかぎり省略する。
(1) 基礎知識「倍音列」

図1 倍音列、第16倍音まで。(wikipediaよりhttp://ja.wikipedia.org/wiki/倍音)
倍音列は根音の周波数を1としてその倍数による周波数の音を並べたものである。正確に平均律の12音と一致する音は1, 2, 4, 8, 16...のオクターヴ音のみなので、この譜例で示された音はあくまでも便宜のために大体の高さを示したものである。根音と同じ周波数を持つ周期性のある振動は、その具体的な波形と関わらず、倍音のサイン音を足すことによって合成的に作ることができるので(フーリエの定理)、倍音が根音の周波数を持つ音楽的な音の構成要素だとも言われる。
聴覚資料
1鋸歯状波の音で順番に奏でられた1から16の倍音(上の譜例の通り)
http://deutsch.c.u-tokyo.ac.jp/~Gottschewski/gaidai/2013/131206/baionretsu.mp3
それ以外の倍音の実験は下記のリンクをご覧下さい。
http://deutsch.c.u-tokyo.ac.jp/~Gottschewski/musik/091016.htm
(2)基礎知識「純正音程」
倍音列の中に出て来る音の相互関係は「純正音程」と言う。純正音程とは、周波数の関係が自然数の比率によって正確に表される音程である。音楽論では特にオクターヴ[1](1対2の比率)、純正5度(2対3の比率)と純正長3度(4対5の比率)がもっとも重要な音程で、後はそこから間接的に発生するものとしても説明できる純正4度(3対4の比率)、純正短3度(5対6の比率)、純正短6度(5対8の比率)、純正長6度(3対5の比率)などがある。7以上の素数を含む自然数による純正音程は西洋音楽で原則として使われない。
(3)基礎知識「ピュタゴラス音律」
純正調の音程で5以上の素数を使わない音組織、つまりオクターヴ関係と五度関係だけで説明できる音組織は「ピュタゴラス音律」という。

図2 ピュタゴラス音律の音組織とその音の主音に対しての従属性・比率。
ピュタゴラス音律は理論的に真ん中から両側に無限に広がって、どんなに行っても絶対にもとの音に戻らないから、1オクターヴ内でも無限のピッチが発生する。しかし実際にはその一部しか使わない。例えば真ん中のC–G–D–A–Eだけを取って五音音階(ドレミソラ)、F–C–G–D–A–E–Bだけを取って七音音階(ハ長調)、E♭–B♭–F–C–G–D–A–E–B–F♯–C♯–G♯だけを取って鍵盤の十二音を得ることができる。この様に純正五度とオクターヴによって五音音階・七音音階・十二音音階を計算するのはギリシア時代から存在していた方法であり、古代中国にも同じ方法が存在した。ただしこれらによって得られた十二音の間に発生する十二の半音は243対256の比率で計算される七つの「短二度」と2048対2187の比率で計算される五つの「増一度」の二種類に分かれ、同等の音程ではない。
(4)基礎知識「平均律」
ピュタゴラス音律で五度を純正五度より僅かに小さめに[2](従って四度を純正四度より僅かに大きめに)取ると、「短二度」と「増一度」を同じ幅にすることができる。そうすればA♭とG♯は同じ音高になり、一オクターヴに十二の音高しか鳴らせない鍵盤楽器でもピュタゴラス音律の無限のピッチを全て弾けるようになる。この方法は「平均律」という。十八~十九世紀以後の鍵盤楽器では一般的にこの方法が取られている。しかし平均律の応用によってA♭とG♯が便宜上同じ音高になっても、調性音楽ではその音楽的な意味が違うので、同じピッチと見なされない。
つまり平均律ではA♭とG♯は「異名同音」になるが、音楽の意味上では「同音」ではなく、「異音」である。そこで「音高」と「音の同一性」を別に考える必要が出てくる。(それに対して純正ピュタゴラス音組織では音の同一性は音高によって完全に決まる。)従って平均律では調性的な意味の違いを前後関係から読み解かなければならない。例えばA♭とG♯のどちらかの意味を持つことができるGとAの間の黒鍵は、旋律でAの前に使われれば、それが普通G♯と解釈される。何故かといえば、G♯からAに進行する場合はその音程は短二度で、調性音楽で一般に旋律に使われる音程である。逆に仮にA♭からAの進行として解釈してみた時にその音程は増一度であり、旋律で一般的に使われる音程ではない。
ピタゴラス音律と平均律の関係から考えられる調性の危機の理由
鍵盤楽器と平均律が普及し、同時に音楽に半音的な旋律進行が多く使われるようになり、調性音楽の解釈に不可欠な異名同音の意味上の区別が徐々に不可能になった。それによって主音にどの様に従属しているかが判別できない音が多くなり、調性(=音楽の和声的な解釈)が曖昧になったことである。
(5)基礎知識 「協和音」としての長短三度
ピュタゴラス音律と平均律の根本的な問題から調性の危機の一つの理由がすでに分かったが、もう一つの重要な理由は、三度を重ねることによって構成される和音(三和音、後で四和音、五和音等も)の多義性にある。
この「三度を重ねること」にはまず、長短三度が協和音として解釈されることが前提である。ピュタゴラス音律からはその理由を数学的にも音響的にも理解できない。つまりその音律で音程を聴き比べれば、例えば長2度や長9度が長3度や長10度よりも協和音に聴こえる。その状況が平均律を使ってもあまり変わらない。実際にピュタゴラス音律を基礎としていた中世音楽や今日までそれを基礎としている雅楽では3度が協和音と見なされない。しかし倍音列に第4倍音と第5倍音の間に生じる4対5の比率を使えば、長3度が圧倒的に協和的になる。(図3で示された聴覚資料を聴けば分かる。)従って「三和音が和声の基礎に置かれること」と「ピュタゴラス音律や平均律から離れて4対5の純正3度を取り入れる」という、西洋音楽史において画期的な二つの変化が必然的な相互関係にある。この変化がルネサンス時代に起こり、16世紀以後の音楽論を特徴付ける。(基礎知識はここまで)
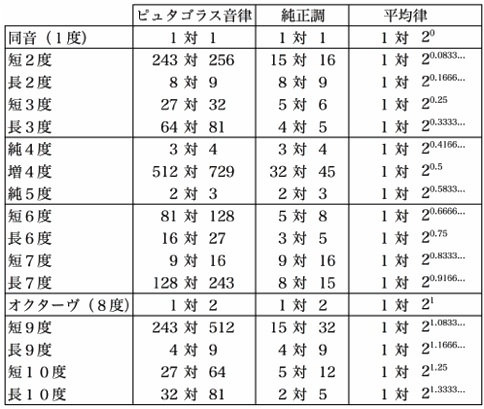
図3 三種類の十二音音階で、主音から見た一度から長10度までの周波数の比率。「ピュラゴラス音律」と「純正調」には無限の音素材があるので、そこから12音の範囲を選ぶのには複数の可能性がある。従ってここで挙げた比率は飽くまでも一例だが、それは「出来る限り小さい数を使う」という原則で選んだ。
聴覚資料:
http://fusehime.c.u-tokyo.ac.jp/gottschewski/doc/pythagoras.mp3
http://fusehime.c.u-tokyo.ac.jp/gottschewski/doc/junseichou.mp3
http://fusehime.c.u-tokyo.ac.jp/gottschewski/doc/heikinritsu.mp3
純正3度(4対5の比率)と純正5度(2対3の比率)の両方を応用したもっとも簡単な音階はドミソとファラドとソシレの三つの三和音(それぞれの周波数の比率を4対5対6)から構成された長音階である。
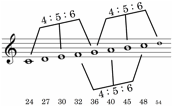
図4 三つの三和音から構成された長音階とその周波数の比率。
しかしこのもっとも簡単なシステムの中でさえ問題が生じる。それはこの音階の中にレ―ラの5度が純正5度ではなく、そこからかなり大きく外れた27対40の比率になっていることである。従って鍵盤楽器の白鍵をこの様にハ長調の基本の和音に従って純正調で調律するとハ長調、ヘ長調、ト長調、イ短調、ホ短調の五つの三和音が純正の音程によって構成されているが、ニ短調の三和音のみがかなり狂った響きをする。

図5 純正調の中で弾かれたハ長調の基本和声。最後の三和音のみが狂っている。
聴覚資料:http://fusehime.c.u-tokyo.ac.jp/gottschewski/doc/3waon.mp3
弦楽器や管楽器の様に、細かい音高の変化が可能な楽器で演奏する場合には、ハ長調の中にこのニ短調の和声が使われる時にD(ニ音)の音を少し低めに演奏して、響きを正すことができる。しかしその結果としてハ長調には二つ以上の「D」が存在し、旋律の中でその音を使う場合には本来どちらを使うかを明らかにしなければならない。そうしなければ主音に対しての従属性に多義性が生じて、少なくとも理論的に調性が危機状態に陥る。
この問題への解決案は近代の音楽論で多く提示されたが、実際の作曲や演奏ではハ長調の二つのDを区別する習慣が普及しなかった。(鍵盤楽器ではそれが不可能だという問題もその背景にあるかもしれない。)ともかく和声の多義性が何の転調もないハ長調の中ですら存在するという事実をここで指摘したい。そしてこの問題が解決しないから結局再び平均律の応用が普及し、三度の協和性が実際の響きと言うより機能的な意味として成立する。
(6)基礎知識 和声における多義性の拡大
上で見たように、三和音を協和音として認めたにもかかわらず、実際に使われる1オクターヴ内の12音は増やされなかったので、音の従属性の可能性が圧倒的に増えた。19世紀以後の和声論[3]ではバッハ以来の作品における和声の意味についての論争が(今日までも)尽きないが、その原因はまさにこの多義性にある。また、作曲家たちがこの多義性を意図的に使い、同じ音高に構成される、異なる意味を持つ和声を、聴者に推測させて、推測された意味と別な意味で解決するなどの技法を使う。それはハイドンがすでに戦略的に使い、シューベルトでより多くなり、ヴァーグナーの作品では徹底されるが、同時にそこで発展の限界が明らかになる。(基礎知識はここまで)
![]()
図6 この譜例で二分音符として書かれた和音は鍵盤ですべて同じに響くが、調性的な意味が全く違う。
聴覚資料:http://fusehime.c.u-tokyo.ac.jp/gottschewski/doc/kaiketsu.mp3
譜例6で示された「減7の和音」は平均律で全く対称的な形をしている(全ての音程が3半音から構成される)ので、その響きだけで調性を推測することができない。また、次の様な変化によって、減7の和音が減7の和音に解決することが可能で、それを徹底させると「和声的に説明可能で意味不明」な和音が続く場合がある。

図7 左の例では減7の和音がそれぞれ解決し(従ってその意味が明らかにされ)、次に別の減7の和音に進行するが、右の例の様に解決が省略されることがある。楽譜では正書法的に意味が明らかにされているが、楽器で弾かれた響きのみを聴けば、図6で示された減7の和音の種類の内どれが使われているかを知ることができない。
聴覚資料:http://fusehime.c.u-tokyo.ac.jp/gottschewski/doc/7waon.mp3
この「7の和声の連続」を徹底的な応用例はショパンの有名な「別れの曲」(練習曲作品10/3)に見られる。

聴覚資料:http://www.youtube.com/watch?v=ISBKq29aksE (1分57秒から)
この様な例では調性音楽としての「意味の可能性」だけが残り、実際の意味が不明である。シュパンがこの作品を書いた19世紀前半にはこういう例はまだ極めて珍しいが、後半ではそういうケースが段々多くなって来る。そして結局聴者も作曲家も和音の中で機能和声と別の意味を見出さなければならない。そこから20世紀の様々な「現代音楽」が現れる。